crypto系列8-国产对称算法SM2

SM2算法

SM2是中国自主设计的椭圆曲线公钥密码算法，主要用于数字签名、密钥交换和公钥加密，是国家密码管理局认定的国密标准算法之一。

一、SM2算法的核心特性

1. 高安全性：基于椭圆曲线离散对数问题（ECDLP），该问题在数学上具有较高的计算复杂度，能有效抵抗当前主流的攻击方式。
2. 高效性能：相比传统的RSA算法，在相同安全等级下，SM2的密钥长度更短（如256位SM2等效于3072位RSA），运算速度更快，更适合资源受限的设备（如物联网终端、智能卡）。
3. 合规性：作为中国《信息安全技术 公钥密码算法第2部分：SM2椭圆曲线公钥密码算法》（GB/T 32918.2-2016）的核心算法，满足国内政务、金融、能源等关键领域的密码合规要求。

二、SM2的主要应用场景

• 数字签名：用于电子合同、电子公文、软件版权认证等场景，确保数据的完整性和发送者身份的真实性。
• 密钥交换：在通信双方（如客户端与服务器）之间安全协商会话密钥，保障后续数据传输的加密安全。
• 公钥加密：对敏感信息（如用户隐私数据、金融交易信息）进行加密，仅授权方（持有私钥）可解密。
• 协同加密：常与国密对称加密算法SM4配合使用，SM2负责密钥分发，SM4负责数据批量加密，形成完整的密码应用体系。

三、核心算法流程

SM2支持三大核心操作，分别是数字签名（含验签）、密钥交换、公钥加密（含解密）。

1. 数字签名与验签流程

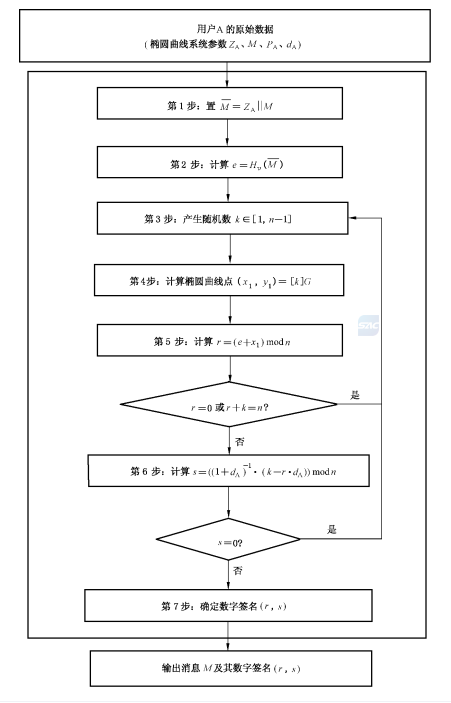
• 签名步骤：
  1. 签名方用SM3哈希算法计算待签名数据的哈希值。
  2. 签名方使用自身私钥，结合随机数和椭圆曲线运算，生成签名值（含两个分量r、s）。
  3. 将待签名数据与签名值（r、s）一同发送给验签方。

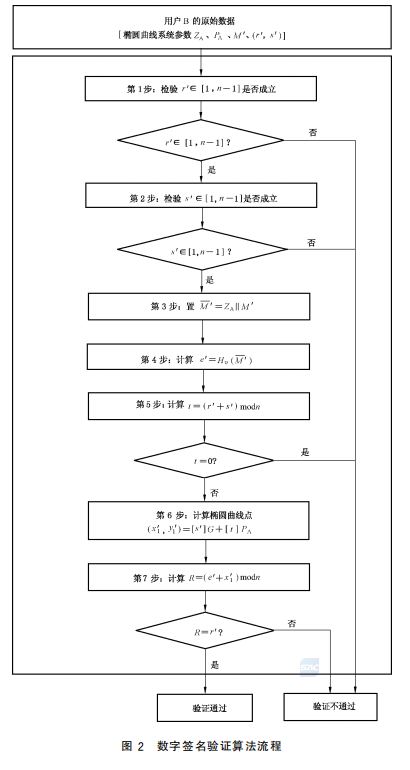
• 验签步骤：
  1. 验签方接收数据后，用相同的SM3算法计算数据哈希值。
  2. 验签方使用签名方的公钥，结合椭圆曲线运算验证签名值（r、s）的合法性。
  3. 若运算结果与签名中的r一致，则验签通过；反之则失败。
     

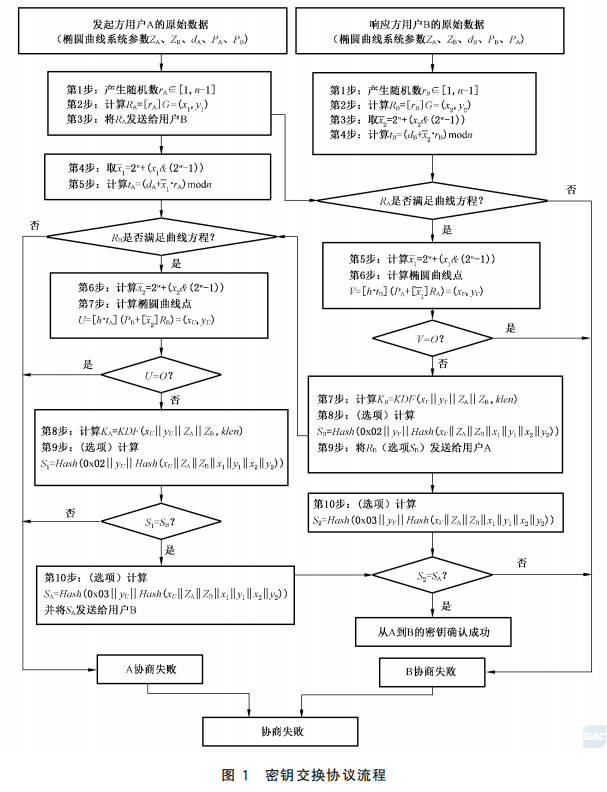
2. 密钥交换流程

1. 通信双方（A、B）分别生成自身的公私钥对，并交换公钥。
2. 双方各自结合自身私钥与对方公钥，通过椭圆曲线点乘法计算出相同的会话密钥。
3. 会话密钥生成后，需用SM3进行哈希处理，确保密钥的一致性和完整性。
   

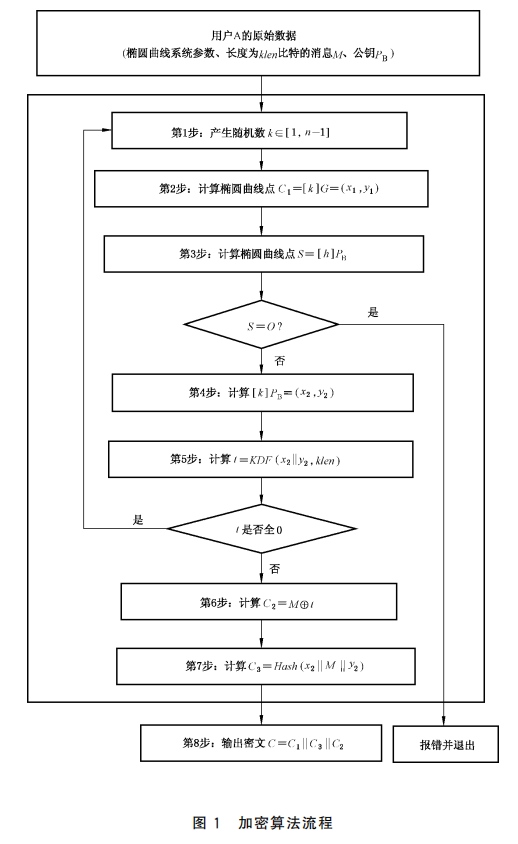
3. 公钥加密与解密流程

• 加密步骤：

  1. 加密方用接收方的公钥，结合随机数和椭圆曲线运算，生成临时公钥和加密密钥。
  2. 用生成的加密密钥对明文数据进行对称加密（通常配合SM4算法），并生成加密数据。
  3. 将临时公钥、加密数据及SM3哈希值（用于完整性校验）一同发送。
     

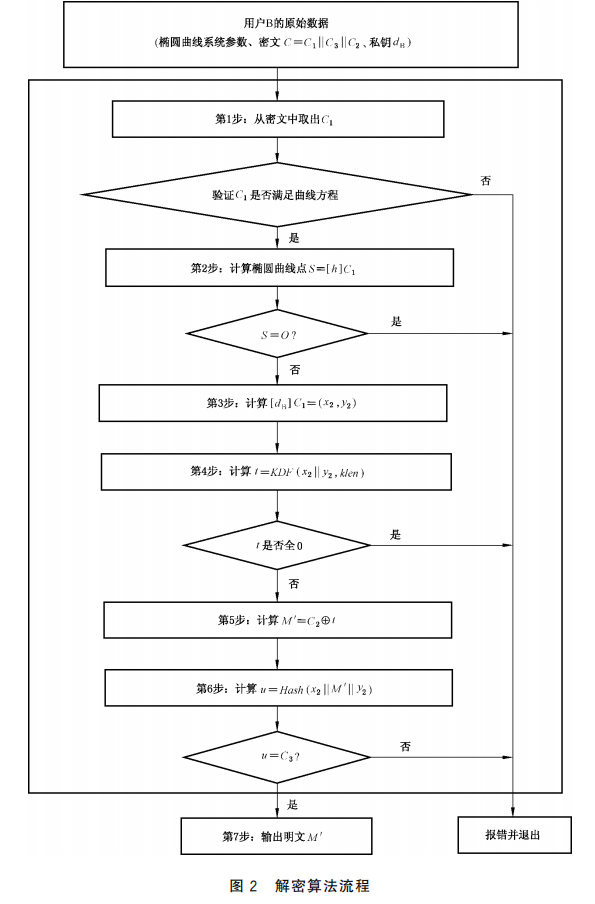
• 解密步骤：

  1. 解密方用自身私钥解析临时公钥，还原出加密密钥。
  2. 用加密密钥解密数据，得到明文，同时通过SM3哈希值验证数据完整性。
  3. 若哈希值匹配则解密成功；反之则数据被篡改，解密失败。
     

四、SM2与RSA算法的关键区别

对比维度	SM2算法	RSA算法
数学基础	椭圆曲线离散对数问题	大整数分解问题
密钥长度（等效安全）	256位	3072位
运算速度	更快（加解密、签名验签）	较慢（大整数运算耗时）
适用场景	国内合规场景、轻量化设备	全球通用场景、兼容性优先

---

行动，才不会被动!

欢迎关注个人公众号 微信 -> 搜索 -> fishmwei，沟通交流。

博客地址： https://fishmwei.github.io

掘金主页： https://juejin.cn/user/2084329776486919

---